グラフを描くことはデータを視覚化し、データについての洞察を得るために不可欠です。“Python”言語でグラフを作成するために使用される有名なライブラリの1つは、Matplotlib (https://matplotlib.org/)です。このライブラリにより、さまざまなタイプのグラフをプロットすることができます。カスタマイズによって、グラフ描画のための様々なオプションを利用することができます。Matplotlibを使用すると、ユーザーは折れ線グラフ (line plot)、棒グラフ (bar plot)、散布図 (scatter plot)、ヒストグラム (histogram)などを作成できます。これにより、プログラマーやデータアナリストは迅速にかつ容易に見栄えの良いグラフを生成することができます。
データを視覚的にグラフで表現することで、パターンやトレンドを簡単に識別および理解できます。さらに、Matplotlibライブラリでは軸の目盛り付けやタイトルの追加、色やスタイルのカスタマイズ、結果のグラフをファイルとして保存して共有することが可能です。全体的に、“Python”プログラミングでMatplotlibの使用方法を習得することは、データ分析や視覚化を行うすべての人々にとって重要なスキルです。
1 Matplotlibライブラリのインポート
Matplotlibライブラリを使用する際には、ほとんどの場合matplotlib.pyplotモジュールが使用されます。このモジュールは、グラフを作成するためのインターフェースを提供します。次の文を使用して、モジュールを”Python”コードにインポートできます:
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = "STIX Two Text"
plt.rcParams["mathtext.fontset"] = "stix"この import 文では、通常、Matplotlibライブラリのpyplotモジュールを参照するためにエイリアス (alias)としてpltを使用します。
NOTE
- エイリアスとは「別名」といった意味です。
pyplotそのものを用いるよりも、シンプルなpltをエイリアスとしてしばしば用います。- モジュールは”Python”コードを含んでいるファイルのことを意味します。
- ライブラリは通常複数のモジュールのセットのことを意味し、特定の機能を提供しています。
2 簡単な折れ線グラフのプロット
2.1 プロットの準備
最も一般的なプロットの1つは、2つの連続変数間の関係を可視化する簡単な折れ線グラフ (line plot)です。Matplotlibでは、 plt.plot() を使用して折れ線グラフを作成できます。以下は、Matplotlibで基本的な折れ線グラフを作成する方法の例です:
x = [1, 2, 3, 4, 5]
y = [2, 3, 5, 7, 11]
fig, ax = plt.subplots(1, 1)
ax.plot(x, y)
この例では、まずMatplotlibライブラリをインポートし、それから x 軸と y 軸の値を表す2つのリストxとyを定義します。その後、plt.subplots()を呼び出します。引数の2と1は行数と列数を決定します。たとえば、次のコードを実行すると、2行1列からなるグラフが作成されます:
plt.subplots(2, 1)
最後に、ax.plot(x, y)を使って、折れ線グラフを作成します。
NOTE: Matplotlibライブラリにおける figure と axis
Matplotlibライブラリでは、軸(axis)と図(figure)の概念がプロットの作成やカスタマイズで重要な役割を果たします。
図(figure)
figureはプロット要素 (グラフなど) が表示される全画像またはウィンドウ全体を表します。- 図のサイズ、解像度、背景色などをカスタマイズできます。
- 1つの
figure内に複数のサブプロットを作成して、1つの図内にさまざまなプロットを表示できます。軸(axis)
- 軸は
figure内部の個々のプロッティング領域を表します。各axesオブジェクトはデータ点、グリッド線、ラベル、およびプロット要素が描画される場所です。- 各
axesオブジェクトには軸の上限や下限、ラベル設定、目盛り設定などグラフの外観をカスタマイズするためのメソッド (method) や属性 (attribute) があります。これまでに紹介した
plt.subplots()を使わずにグラフを描画することも可能です:x = [1, 2, 3, 4, 5] y = [2, 3, 5, 7, 11] plt.plot(x, y)
しかしながら、
plt.subplots()は将来的により複雑な図を作成するにあたって応用することができますので、ここで紹介しています。
2.2 プロットのカスタマイズ
プロットの可読性と視覚的な印象を向上させるために、ラベル、タイトル、色などを追加してカスタマイズすることができます。以下はプロットをカスタマイズする方法です:
fig, ax = plt.subplots(1, 1)
ax.plot(x, y, color='green', marker='o', linestyle='--')
ax.set_xlabel('$x$-axis label')
ax.set_ylabel('$y$-axis label')
ax.set_title('Simple Line Plot')Text(0.5, 1.0, 'Simple Line Plot')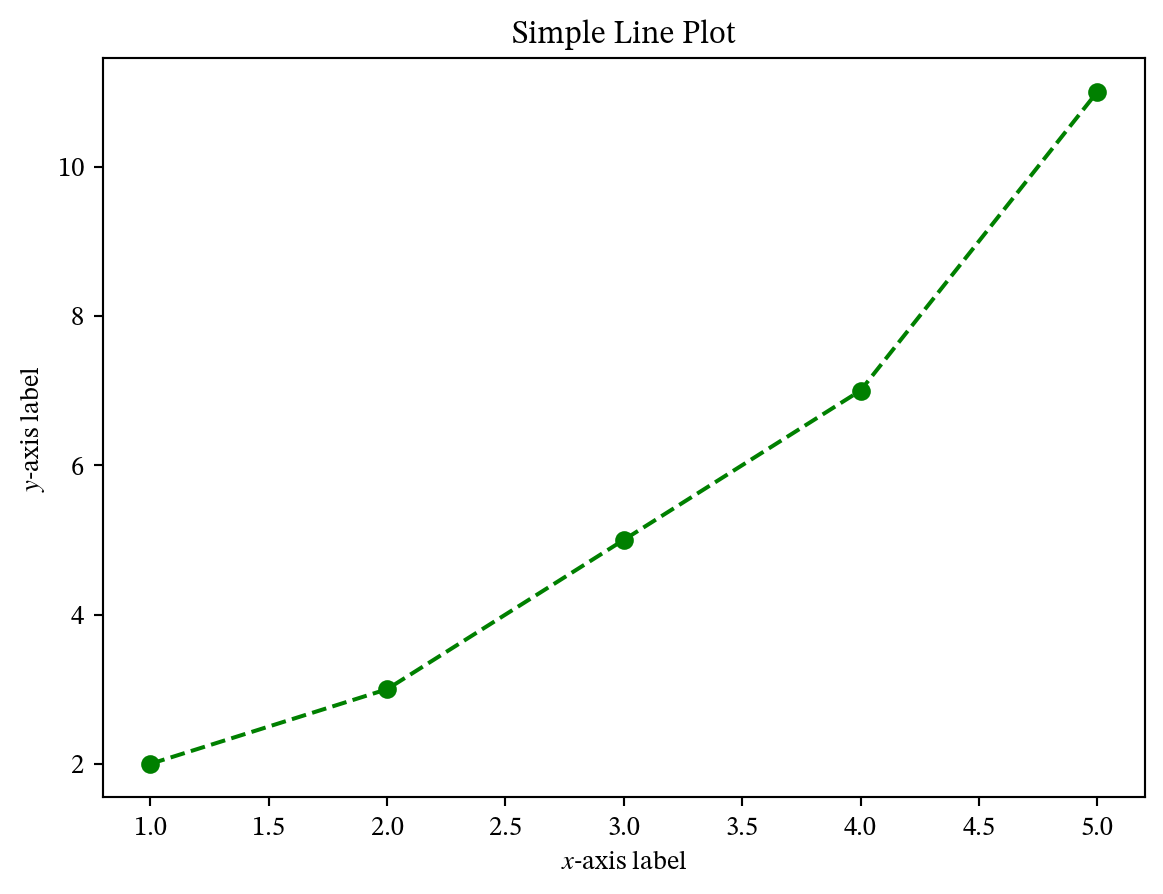
このカスタマイズされたプロットでは、線の色を緑に指定し、marker='o'で円形のマーカーを追加し、linestyle='--'で線のスタイルを点線に設定しています。さらに、 x 軸と y 軸にラベルを追加するためにそれぞれax.set_xlabel()とax.set_ylabel()を使用しています。プロットにはax.set_title()でタイトルが付けられています。プロットで使用されるフォントを変更することもできます。
NOTE
プロット内で数式を使用することができます。たとえば、
$x$は数式内の文字として表示されます。数式用のフォントを変更するには、plt.rcParams['mathtext.fontset'] = 'FONT'を使用できます。
3 関数のグラフをプロットする
関数のグラフをプロットすることは、数学的における関数を簡単に視覚化して理解するための便利な方法です。
NOTE: 数学における関数
数学では、関数とは入力(定義域)の集合と出力(値域)の集合との間の関係であり、各入力が正確に1つの出力に関連付けられるものです。もし1つの入力に複数の出力がある場合、それは関数ではありません。関数はしばしば f(x) or y = f(x) と表されます。ここで、 x は入力を示し、 f(x) は出力を示しています。
一次関数 y = 2x + 3, x \in \mathbb R のグラフを描くことから始めます。ここで、定義域は x\in \mathbb R で、全ての実数を表します。まず、defキーワードを使用して数学における関数を定義します:
def f(x):
return 2*x + 3この関数に入力を渡すと、出力が返されます:
print(f(1))
print(f(2))
print(f(-1))5
7
1数学関連のプログラミングを行う際には、NumPy (https://numpy.org/)ライブラリが非常に便利です。しかしこの記事では、このクラッシュコースで学んだ内容を復習するために組み込みリストを使用します。
次に、グラフのための入力値を準備します:
xs = [-5 + 0.01*i for i in range(1000)]
print(min(xs))
print(max(xs))-5.0
4.99このコードは -5 と 5 の間で1000個の少数を生成します。 次に xs を入力することにより、出力が生成されます:
ys = [f(x) for x in xs]
print(ys)[-7.0, -6.98, -6.960000000000001, -6.9399999999999995, -6.92, -6.9, -6.880000000000001, -6.859999999999999, -6.84, -6.82, -6.800000000000001, -6.779999999999999, -6.76, -6.74, -6.720000000000001, -6.699999999999999, -6.68, -6.66, -6.640000000000001, -6.619999999999999, -6.6, -6.58, -6.5600000000000005, -6.539999999999999, -6.52, -6.5, -6.48, -6.460000000000001, -6.4399999999999995, -6.42, -6.4, -6.380000000000001, -6.359999999999999, -6.34, -6.32, -6.300000000000001, -6.279999999999999, -6.26, -6.24, -6.220000000000001, -6.199999999999999, -6.18, -6.16, -6.140000000000001, -6.119999999999999, -6.1, -6.08, -6.0600000000000005, -6.039999999999999, -6.02, -6.0, -5.98, -5.960000000000001, -5.9399999999999995, -5.92, -5.9, -5.879999999999999, -5.859999999999999, -5.84, -5.82, -5.800000000000001, -5.779999999999999, -5.76, -5.74, -5.720000000000001, -5.699999999999999, -5.68, -5.66, -5.640000000000001, -5.619999999999999, -5.6, -5.58, -5.5600000000000005, -5.539999999999999, -5.52, -5.5, -5.48, -5.460000000000001, -5.4399999999999995, -5.42, -5.4, -5.379999999999999, -5.359999999999999, -5.34, -5.32, -5.300000000000001, -5.279999999999999, -5.26, -5.24, -5.220000000000001, -5.199999999999999, -5.18, -5.16, -5.140000000000001, -5.119999999999999, -5.1, -5.08, -5.0600000000000005, -5.039999999999999, -5.02, -5.0, -4.98, -4.96, -4.9399999999999995, -4.92, -4.9, -4.88, -4.859999999999999, -4.84, -4.82, -4.8, -4.779999999999999, -4.76, -4.74, -4.72, -4.699999999999999, -4.68, -4.66, -4.640000000000001, -4.62, -4.6, -4.58, -4.5600000000000005, -4.54, -4.52, -4.5, -4.48, -4.46, -4.4399999999999995, -4.42, -4.4, -4.38, -4.359999999999999, -4.34, -4.32, -4.3, -4.279999999999999, -4.26, -4.24, -4.22, -4.199999999999999, -4.18, -4.16, -4.140000000000001, -4.12, -4.1, -4.08, -4.0600000000000005, -4.04, -4.02, -4.0, -3.9800000000000004, -3.96, -3.9399999999999995, -3.92, -3.9000000000000004, -3.88, -3.8599999999999994, -3.84, -3.8200000000000003, -3.8, -3.7799999999999994, -3.76, -3.74, -3.7199999999999998, -3.6999999999999993, -3.6799999999999997, -3.66, -3.6400000000000006, -3.62, -3.5999999999999996, -3.58, -3.5600000000000005, -3.54, -3.5199999999999996, -3.5, -3.4800000000000004, -3.46, -3.4399999999999995, -3.42, -3.4000000000000004, -3.38, -3.3599999999999994, -3.34, -3.3200000000000003, -3.3, -3.2799999999999994, -3.26, -3.24, -3.2199999999999998, -3.1999999999999993, -3.1799999999999997, -3.16, -3.1400000000000006, -3.12, -3.0999999999999996, -3.08, -3.0600000000000005, -3.04, -3.0199999999999996, -3.0, -2.9799999999999995, -2.96, -2.9399999999999995, -2.92, -2.9000000000000004, -2.88, -2.8600000000000003, -2.84, -2.8200000000000003, -2.8, -2.7800000000000002, -2.76, -2.74, -2.7199999999999998, -2.7, -2.6799999999999997, -2.66, -2.6399999999999997, -2.62, -2.5999999999999996, -2.58, -2.5599999999999996, -2.54, -2.5199999999999996, -2.5, -2.4799999999999995, -2.46, -2.4399999999999995, -2.42, -2.3999999999999995, -2.38, -2.3600000000000003, -2.34, -2.3200000000000003, -2.3, -2.2800000000000002, -2.26, -2.24, -2.2199999999999998, -2.2, -2.1799999999999997, -2.16, -2.1399999999999997, -2.12, -2.0999999999999996, -2.08, -2.0599999999999996, -2.04, -2.0199999999999996, -2.0, -1.9799999999999995, -1.96, -1.9399999999999995, -1.92, -1.8999999999999995, -1.88, -1.8600000000000003, -1.8399999999999999, -1.8200000000000003, -1.7999999999999998, -1.7800000000000002, -1.7599999999999998, -1.7400000000000002, -1.7199999999999998, -1.7000000000000002, -1.6799999999999997, -1.6600000000000001, -1.6399999999999997, -1.62, -1.5999999999999996, -1.58, -1.5599999999999996, -1.54, -1.5199999999999996, -1.5, -1.4799999999999995, -1.46, -1.4399999999999995, -1.42, -1.3999999999999995, -1.38, -1.3600000000000003, -1.3399999999999999, -1.3200000000000003, -1.2999999999999998, -1.2800000000000002, -1.2599999999999998, -1.2400000000000002, -1.2199999999999998, -1.2000000000000002, -1.1799999999999997, -1.1600000000000001, -1.1399999999999997, -1.12, -1.0999999999999996, -1.08, -1.0599999999999996, -1.04, -1.0199999999999996, -1.0, -0.9799999999999995, -0.96, -0.9399999999999995, -0.9199999999999999, -0.8999999999999995, -0.8799999999999999, -0.8599999999999994, -0.8399999999999999, -0.8200000000000003, -0.7999999999999998, -0.7800000000000002, -0.7599999999999998, -0.7400000000000002, -0.7199999999999998, -0.7000000000000002, -0.6799999999999997, -0.6600000000000001, -0.6399999999999997, -0.6200000000000001, -0.5999999999999996, -0.5800000000000001, -0.5599999999999996, -0.54, -0.5199999999999996, -0.5, -0.47999999999999954, -0.45999999999999996, -0.4399999999999995, -0.41999999999999993, -0.39999999999999947, -0.3799999999999999, -0.35999999999999943, -0.33999999999999986, -0.3200000000000003, -0.2999999999999998, -0.28000000000000025, -0.2599999999999998, -0.2400000000000002, -0.21999999999999975, -0.20000000000000018, -0.17999999999999972, -0.16000000000000014, -0.13999999999999968, -0.1200000000000001, -0.09999999999999964, -0.08000000000000007, -0.05999999999999961, -0.040000000000000036, -0.019999999999999574, 0.0, 0.020000000000000462, 0.040000000000000036, 0.0600000000000005, 0.08000000000000007, 0.10000000000000053, 0.1200000000000001, 0.14000000000000057, 0.16000000000000014, 0.17999999999999972, 0.20000000000000018, 0.21999999999999975, 0.2400000000000002, 0.2599999999999998, 0.28000000000000025, 0.2999999999999998, 0.3200000000000003, 0.33999999999999986, 0.3600000000000003, 0.3799999999999999, 0.40000000000000036, 0.41999999999999993, 0.4400000000000004, 0.45999999999999996, 0.4800000000000004, 0.5, 0.5200000000000005, 0.54, 0.5600000000000005, 0.5800000000000001, 0.6000000000000005, 0.6200000000000001, 0.6400000000000006, 0.6600000000000001, 0.6799999999999997, 0.7000000000000002, 0.7199999999999998, 0.7400000000000002, 0.7599999999999998, 0.7800000000000002, 0.7999999999999998, 0.8200000000000003, 0.8399999999999999, 0.8600000000000003, 0.8799999999999999, 0.9000000000000004, 0.9199999999999999, 0.9400000000000004, 0.96, 0.9800000000000004, 1.0, 1.0199999999999996, 1.040000000000001, 1.0600000000000005, 1.08, 1.0999999999999996, 1.120000000000001, 1.1400000000000006, 1.1600000000000001, 1.1799999999999997, 1.1999999999999993, 1.2200000000000006, 1.2400000000000002, 1.2599999999999998, 1.2799999999999994, 1.3000000000000007, 1.3200000000000003, 1.3399999999999999, 1.3599999999999994, 1.3800000000000008, 1.4000000000000004, 1.42, 1.4399999999999995, 1.4600000000000009, 1.4800000000000004, 1.5, 1.5199999999999996, 1.540000000000001, 1.5600000000000005, 1.58, 1.5999999999999996, 1.620000000000001, 1.6400000000000006, 1.6600000000000001, 1.6799999999999997, 1.700000000000001, 1.7200000000000006, 1.7400000000000002, 1.7599999999999998, 1.7799999999999994, 1.8000000000000007, 1.8200000000000003, 1.8399999999999999, 1.8599999999999994, 1.8800000000000008, 1.9000000000000004, 1.92, 1.9399999999999995, 1.9600000000000009, 1.9800000000000004, 2.0, 2.0199999999999996, 2.040000000000001, 2.0600000000000005, 2.08, 2.0999999999999996, 2.120000000000001, 2.1400000000000006, 2.16, 2.1799999999999997, 2.200000000000001, 2.2200000000000006, 2.24, 2.26, 2.2799999999999994, 2.3000000000000007, 2.3200000000000003, 2.34, 2.3599999999999994, 2.380000000000001, 2.4000000000000004, 2.42, 2.4399999999999995, 2.460000000000001, 2.4800000000000004, 2.5, 2.5199999999999996, 2.540000000000001, 2.5600000000000005, 2.58, 2.5999999999999996, 2.620000000000001, 2.6400000000000006, 2.66, 2.6799999999999997, 2.700000000000001, 2.7200000000000006, 2.74, 2.76, 2.7799999999999994, 2.8000000000000007, 2.8200000000000003, 2.84, 2.8599999999999994, 2.880000000000001, 2.9000000000000004, 2.92, 2.9399999999999995, 2.960000000000001, 2.9800000000000004, 3.0, 3.0199999999999996, 3.040000000000001, 3.0600000000000005, 3.08, 3.0999999999999996, 3.120000000000001, 3.1400000000000006, 3.16, 3.1799999999999997, 3.200000000000001, 3.2200000000000006, 3.24, 3.26, 3.2799999999999994, 3.3000000000000007, 3.3200000000000003, 3.34, 3.3599999999999994, 3.380000000000001, 3.4000000000000004, 3.42, 3.4399999999999995, 3.460000000000001, 3.4800000000000004, 3.5, 3.5199999999999996, 3.540000000000001, 3.5600000000000005, 3.58, 3.5999999999999996, 3.620000000000001, 3.6400000000000006, 3.66, 3.6799999999999997, 3.700000000000001, 3.7200000000000006, 3.74, 3.76, 3.7799999999999994, 3.8000000000000007, 3.8200000000000003, 3.84, 3.8599999999999994, 3.880000000000001, 3.9000000000000004, 3.92, 3.9399999999999995, 3.960000000000001, 3.9800000000000004, 4.0, 4.02, 4.040000000000001, 4.0600000000000005, 4.08, 4.1, 4.120000000000001, 4.140000000000001, 4.16, 4.18, 4.200000000000001, 4.220000000000001, 4.24, 4.26, 4.279999999999999, 4.300000000000001, 4.32, 4.34, 4.359999999999999, 4.380000000000001, 4.4, 4.42, 4.4399999999999995, 4.460000000000001, 4.48, 4.5, 4.52, 4.540000000000001, 4.5600000000000005, 4.58, 4.6, 4.620000000000001, 4.640000000000001, 4.66, 4.68, 4.700000000000001, 4.720000000000001, 4.74, 4.76, 4.779999999999999, 4.800000000000001, 4.82, 4.84, 4.859999999999999, 4.880000000000001, 4.9, 4.92, 4.9399999999999995, 4.960000000000001, 4.98, 5.0, 5.02, 5.040000000000001, 5.0600000000000005, 5.08, 5.1, 5.120000000000001, 5.140000000000001, 5.16, 5.18, 5.200000000000001, 5.220000000000001, 5.24, 5.26, 5.280000000000001, 5.300000000000001, 5.32, 5.34, 5.359999999999999, 5.380000000000001, 5.4, 5.42, 5.4399999999999995, 5.460000000000001, 5.48, 5.5, 5.52, 5.540000000000001, 5.5600000000000005, 5.58, 5.6, 5.620000000000001, 5.640000000000001, 5.66, 5.68, 5.700000000000001, 5.720000000000001, 5.74, 5.76, 5.780000000000001, 5.800000000000001, 5.82, 5.84, 5.859999999999999, 5.880000000000001, 5.9, 5.92, 5.9399999999999995, 5.960000000000001, 5.98, 6.0, 6.02, 6.040000000000001, 6.0600000000000005, 6.08, 6.1, 6.120000000000001, 6.140000000000001, 6.16, 6.18, 6.200000000000001, 6.220000000000001, 6.24, 6.26, 6.280000000000001, 6.300000000000001, 6.32, 6.34, 6.359999999999999, 6.380000000000001, 6.4, 6.42, 6.4399999999999995, 6.460000000000001, 6.48, 6.5, 6.52, 6.540000000000001, 6.5600000000000005, 6.58, 6.6, 6.620000000000001, 6.640000000000001, 6.66, 6.68, 6.700000000000001, 6.720000000000001, 6.74, 6.76, 6.780000000000001, 6.800000000000001, 6.82, 6.84, 6.859999999999999, 6.880000000000001, 6.9, 6.92, 6.9399999999999995, 6.960000000000001, 6.98, 7.0, 7.02, 7.040000000000001, 7.0600000000000005, 7.08, 7.1, 7.120000000000001, 7.140000000000001, 7.16, 7.18, 7.200000000000001, 7.220000000000001, 7.24, 7.26, 7.280000000000001, 7.300000000000001, 7.32, 7.34, 7.359999999999999, 7.380000000000001, 7.4, 7.42, 7.4399999999999995, 7.460000000000001, 7.48, 7.5, 7.52, 7.540000000000001, 7.5600000000000005, 7.58, 7.6, 7.620000000000001, 7.640000000000001, 7.66, 7.68, 7.700000000000001, 7.720000000000001, 7.74, 7.76, 7.780000000000001, 7.800000000000001, 7.82, 7.84, 7.859999999999999, 7.880000000000001, 7.9, 7.92, 7.9399999999999995, 7.960000000000001, 7.98, 8.0, 8.02, 8.040000000000001, 8.06, 8.08, 8.1, 8.120000000000001, 8.14, 8.16, 8.18, 8.200000000000001, 8.22, 8.24, 8.26, 8.280000000000001, 8.3, 8.32, 8.34, 8.36, 8.38, 8.4, 8.42, 8.44, 8.46, 8.48, 8.5, 8.52, 8.540000000000001, 8.56, 8.58, 8.6, 8.620000000000001, 8.64, 8.66, 8.68, 8.700000000000001, 8.72, 8.74, 8.76, 8.780000000000001, 8.8, 8.82, 8.84, 8.860000000000001, 8.88, 8.9, 8.92, 8.94, 8.96, 8.98, 9.0, 9.02, 9.04, 9.059999999999999, 9.080000000000002, 9.100000000000001, 9.120000000000001, 9.14, 9.16, 9.18, 9.2, 9.219999999999999, 9.240000000000002, 9.260000000000002, 9.280000000000001, 9.3, 9.32, 9.34, 9.36, 9.379999999999999, 9.399999999999999, 9.420000000000002, 9.440000000000001, 9.46, 9.48, 9.5, 9.52, 9.54, 9.559999999999999, 9.580000000000002, 9.600000000000001, 9.620000000000001, 9.64, 9.66, 9.68, 9.7, 9.719999999999999, 9.740000000000002, 9.760000000000002, 9.780000000000001, 9.8, 9.82, 9.84, 9.86, 9.879999999999999, 9.899999999999999, 9.920000000000002, 9.940000000000001, 9.96, 9.98, 10.0, 10.02, 10.04, 10.059999999999999, 10.080000000000002, 10.100000000000001, 10.120000000000001, 10.14, 10.16, 10.18, 10.2, 10.219999999999999, 10.240000000000002, 10.260000000000002, 10.280000000000001, 10.3, 10.32, 10.34, 10.36, 10.379999999999999, 10.400000000000002, 10.420000000000002, 10.440000000000001, 10.46, 10.48, 10.5, 10.52, 10.54, 10.559999999999999, 10.580000000000002, 10.600000000000001, 10.620000000000001, 10.64, 10.66, 10.68, 10.7, 10.719999999999999, 10.740000000000002, 10.760000000000002, 10.780000000000001, 10.8, 10.82, 10.84, 10.86, 10.879999999999999, 10.900000000000002, 10.920000000000002, 10.940000000000001, 10.96, 10.98, 11.0, 11.02, 11.04, 11.059999999999999, 11.080000000000002, 11.100000000000001, 11.120000000000001, 11.14, 11.16, 11.18, 11.2, 11.219999999999999, 11.240000000000002, 11.260000000000002, 11.280000000000001, 11.3, 11.32, 11.34, 11.36, 11.379999999999999, 11.400000000000002, 11.420000000000002, 11.440000000000001, 11.46, 11.48, 11.5, 11.52, 11.54, 11.559999999999999, 11.580000000000002, 11.600000000000001, 11.620000000000001, 11.64, 11.66, 11.68, 11.7, 11.719999999999999, 11.740000000000002, 11.760000000000002, 11.780000000000001, 11.8, 11.82, 11.84, 11.86, 11.879999999999999, 11.900000000000002, 11.920000000000002, 11.940000000000001, 11.96, 11.98, 12.0, 12.02, 12.04, 12.059999999999999, 12.080000000000002, 12.100000000000001, 12.120000000000001, 12.14, 12.16, 12.18, 12.2, 12.219999999999999, 12.240000000000002, 12.260000000000002, 12.280000000000001, 12.3, 12.32, 12.34, 12.36, 12.379999999999999, 12.400000000000002, 12.420000000000002, 12.440000000000001, 12.46, 12.48, 12.5, 12.52, 12.54, 12.559999999999999, 12.580000000000002, 12.600000000000001, 12.620000000000001, 12.64, 12.66, 12.68, 12.7, 12.719999999999999, 12.740000000000002, 12.760000000000002, 12.780000000000001, 12.8, 12.82, 12.84, 12.86, 12.879999999999999, 12.900000000000002, 12.920000000000002, 12.940000000000001, 12.96, 12.98]では、 y = 2x + 3 のグラフを視覚化してみましょう。
fig, ax = plt.subplots(1, 1)
ax.plot(xs, ys, color='grey')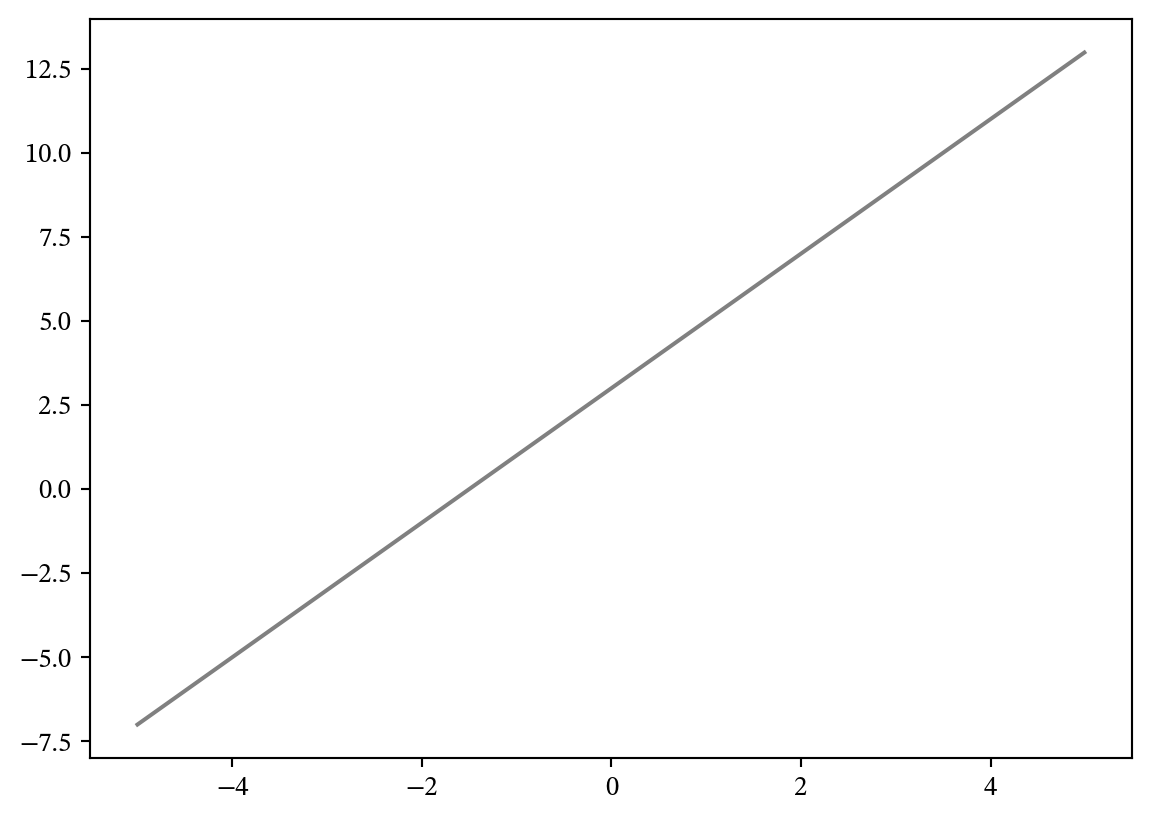
グラフを描くことはできましたが、あまり格好よくは見えません。プロットをカスタマイズしてみましょう:
fig, ax = plt.subplots(1, 1, dpi=150)
ax.plot(xs, ys, color='red', linewidth=0.8)
# アスペクト比を等しく設定
fig.gca().set_aspect('equal', adjustable='box')
# 軸の目盛りラベルのフォントサイズを変更
ax.tick_params(axis='both', which='major', labelsize=5)
# 軸にグリッドを追加
ax.grid(True, linewidth=0.3)
# x軸とy軸を追加
ax.axhline(0, color='black', linewidth=0.6)
ax.axvline(0, color='black', linewidth=0.6)
# 関数名を追加
ax.text(1.5, 12, '$y = 2x + 3$', fontsize=8)
# 各軸の上限と下限を設定
ax.set_xlim(min(xs), max(xs))
ax.set_ylim(min(ys)-1, max(ys)+1)
# 目盛り間隔を設定
ax.set_xticks([x for x in range(int(min(xs)), int(max(xs))+2)])
ax.set_yticks([y for y in range(int(min(ys))-1, int(max(ys))+3)])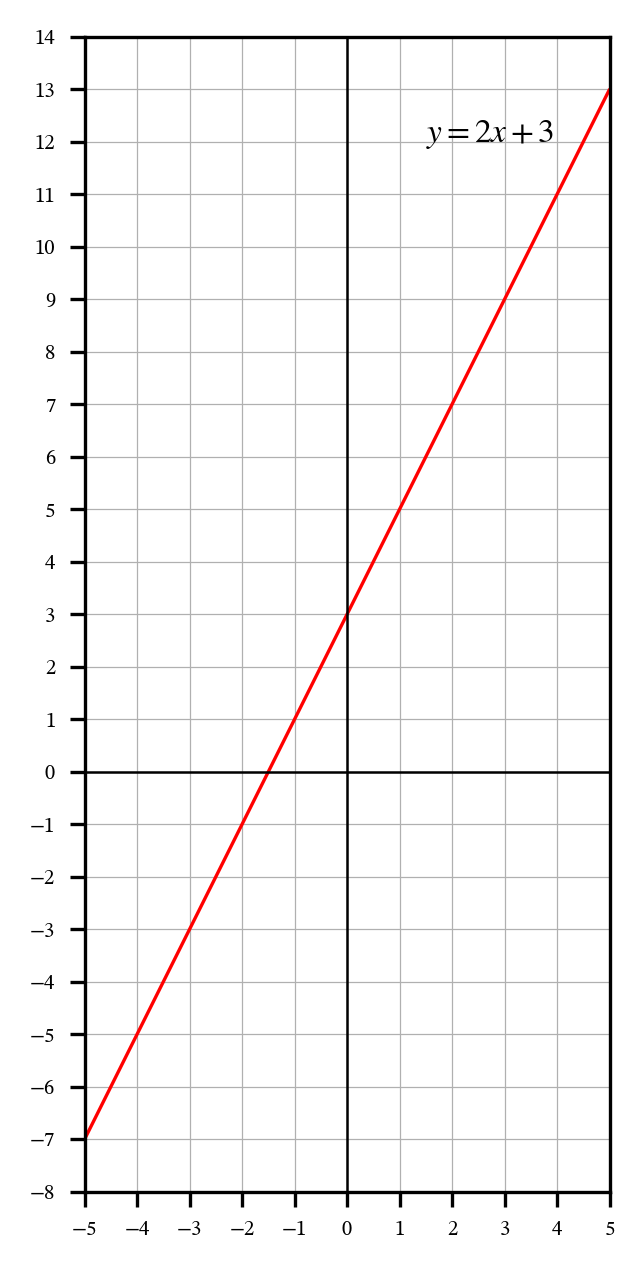
この新しいグラフはどうでしょうか?数学における関数のグラフを視覚化する点においては、前のものよりもずっと優れていると思います。
数学における関数のグラフを描画するたびに上記のカスタマイズしたコードを書くことは、本当に面倒だと思うかもしれません。心配しないでください、“Python”言語の関数を利用することができます。
これが数学における関数のグラフを描画するための例です。テキストを表示する位置のオプションを受け取るために **kwargs を使用しています。これはこのクラッシュコースの範囲外なので気にしないでください。
def plot_math_function(func, x_min, x_max, **kwargs):
"""
数学関数のグラフを描画します
Args:
- func: 描画する数学関数
- x_min: ドメインの最小値としてのxの値
- x_max: ドメインの最大値としてのxの値
- **kwargs: プロットをカスタマイズするために渡すことができる追加のキーワード引数
- x_pos: 関数名のx座標
- y_pos: 関数名のy座標
- label: プロットに表示される関数名
Returns:
- figure
- axis
"""
# 関数名用のオプションです
options = {
'label': '',
'x_pos': x_max-1,
'y_pos': func(x_max-1)
}
options.update(kwargs)
# プロットデータを生成します
step = 0.01
num_iter = int((x_max - x_min) / step)
xs = [x_min + step*i for i in range(num_iter)]
ys = [func(x) for x in xs]
fig, ax = plt.subplots(1, 1, dpi=150)
ax.plot(xs, ys, color='red', linewidth=0.8)
# アスペクト比を等しく設定します
fig.gca().set_aspect('equal', adjustable='box')
# 軸目盛りラベルのフォントサイズを変更します
ax.tick_params(axis='both', which='major', labelsize=5)
# 軸にグリッドを追加します
ax.grid(True, linewidth=0.3)
# x軸、y軸を追加します
ax.axhline(0, color='black', linewidth=0.6)
ax.axvline(0, color='black', linewidth=0.6)
# 指定した位置に関数名を追加し、与えられたラベルとフォントサイズで表示します
ax.text(
options.get('x_pos'), # テキスト用のx座標
options.get('y_pos'), # テキスト用のy座標
options.get('label'), # 表示するテキスト
fontsize=8 # 文字サイズ
)
# 各軸(axis)の上限と下限を設定します
ax.set_xlim(min(xs), max(xs))
ax.set_ylim(min(ys)-1, max(ys)+1)
# 目盛りの間隔を設定します
ax.set_xticks([x for x in range(int(min(xs)), int(max(xs))+2)])
ax.set_yticks([y for y in range(int(min(ys))-1, int(max(ys))+3)])
return fig, ax以前のコードを編集して、この関数を作成しました。 この関数を理解するために違いを確認してください。
g()とh()という2つの関数を定義し、それらをプロットします。
def g(x):
return x**2 - 3
def h(x):
return 1/x
plot_math_function(g, -5, 5, label='$y=x^2$', x_pos=2, y_pos=22)
plot_math_function(h, 0.1, 10, label=r'$y=\frac{1}{x}$', y_pos=1)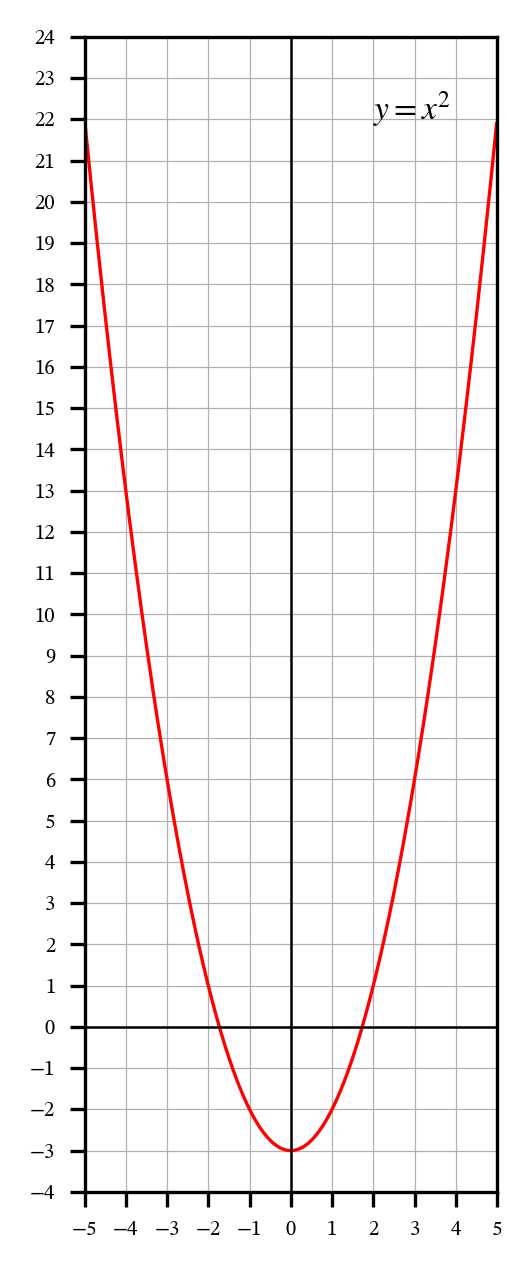
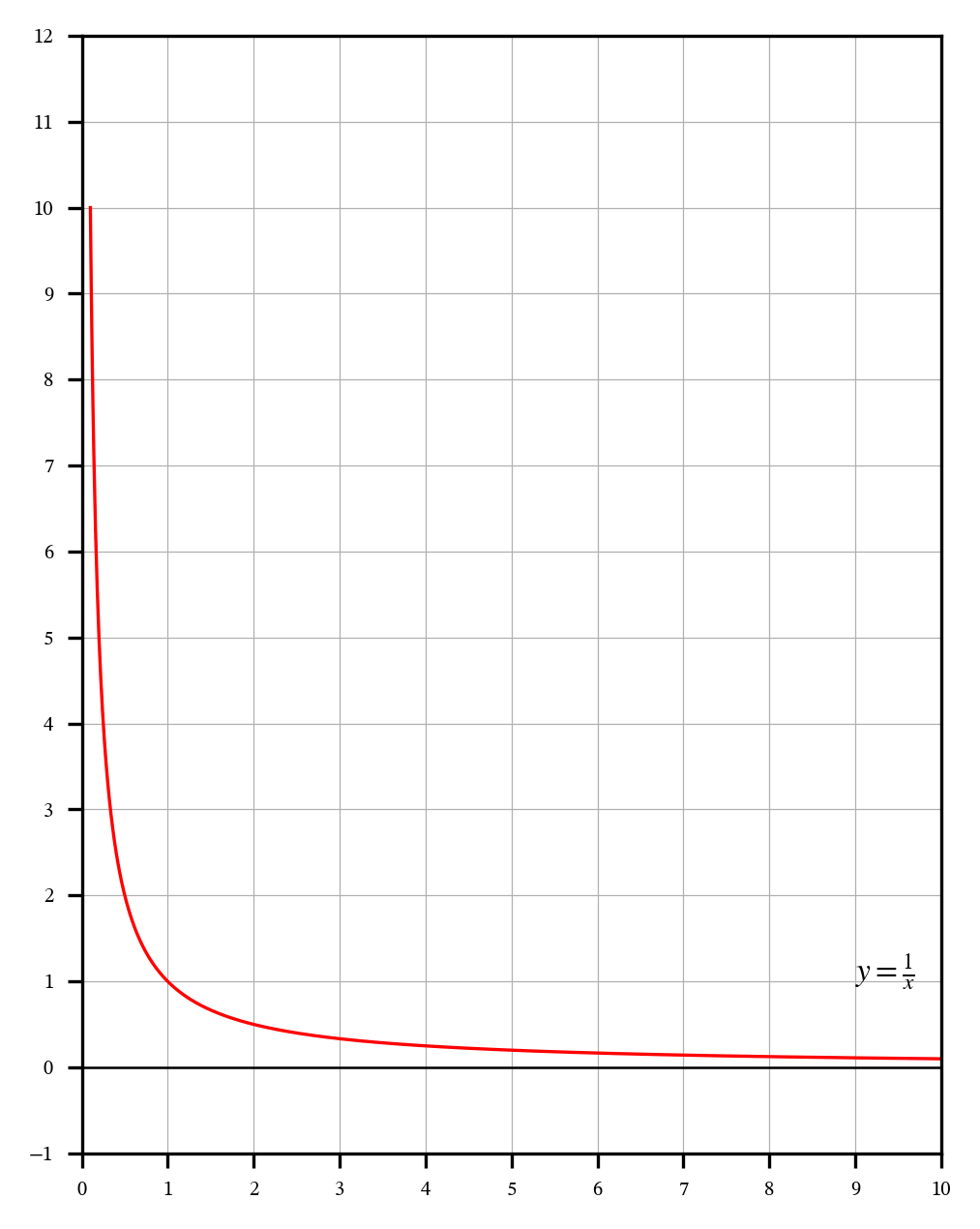
plot_math_function() を使うことにより、毎回カスタマイズすることなしに新しい関数をプロットすることができます。
4 まとめ
棒グラフや箱ひげ図、ヒストグラムなど、他にも多くの種類のグラフがありますが、“Python”言語を使用してグラフを描画する方法を学びました。